Asusetic
0%

AGC008E Next or Nextnext

发表于 分类于 ， ， Valine：
本文字数： 685 阅读时长 ≈ 1 分钟

AGC好题

因为我是从图论题单发现的所以就按图论思考了

先按套路 i→pii \rightarrow p_i 连边，会构成若干个环

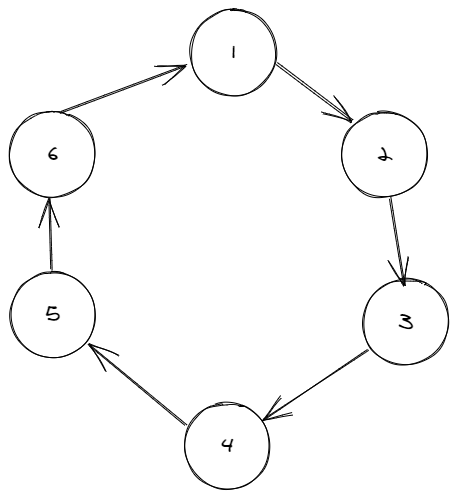
Case0

发现没啥能用的性质

然后 aia_i 的个很好的东西，因为 pip_i 要么是 aia_i 要么下一个是 aia_i 图上表示就类似

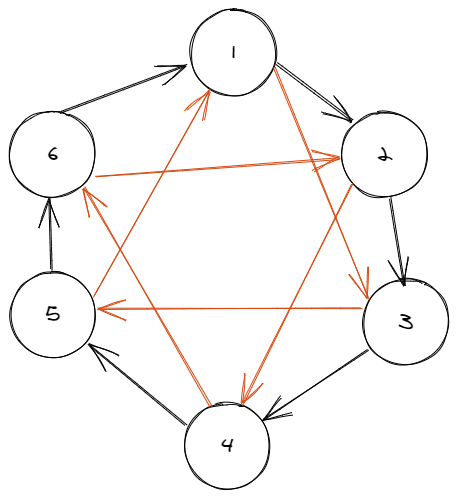
Case1

如果每个 pi=aip_i=a_i 都成立，那就是原图了

同样的每个 ppi=aip_{p_i}=a_i 都成立就是

Case1

这里需要讨论一下，环长位偶数的话像上图会把原图拆成两个大小为一半的环

如果是奇数则

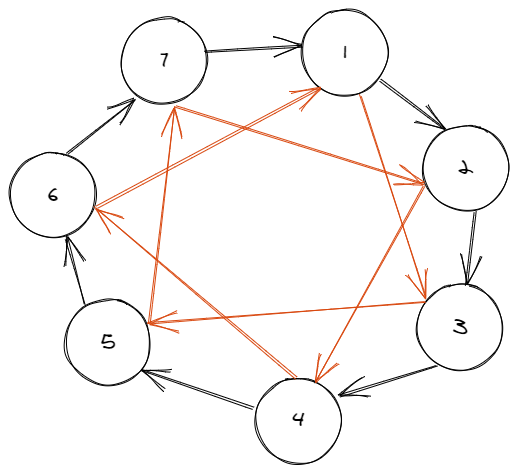
Case1

拉平看一下

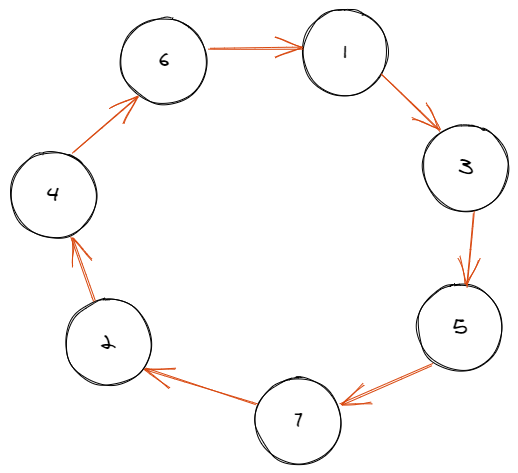
Case1

可以发现这个结构和原图是一样的

最后如果既有 pi=aip_i=a_i ppi=aip_{p_i}=a_i 就是

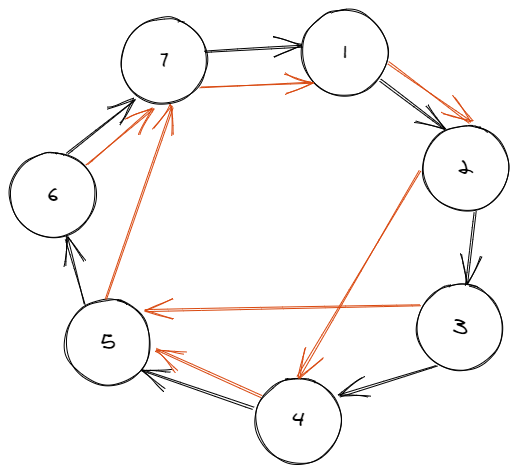
Case1

拉直

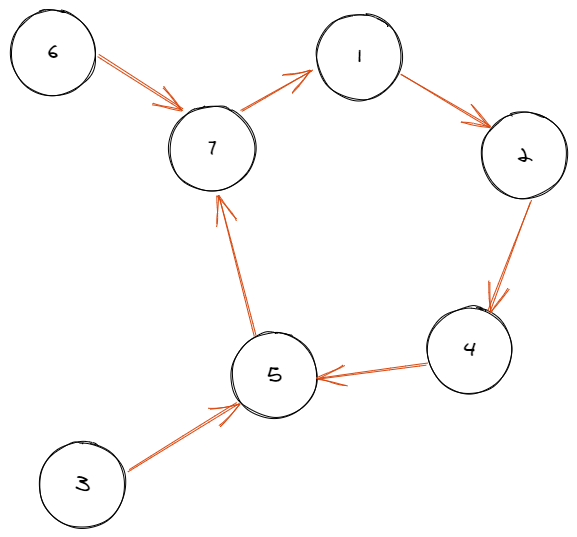
Case1

是一个内向基环树

现在我们拿到了变换完的 i→aii \rightarrow a_i 的图，求原图的方案数

环和基环树没啥关系也不能相互作用

所以分别处理

环的部分考虑dp

dps,kdp_{s,k} 表示大小为 ss 的环考虑到第 kk 个，如果 ss 是奇数那么可以有一个和原图同构的图和原图，即 dps,k−1+dps,k−1dp_{s,k-1}+dp_{s,k-1}

同时也可以向上合并成大环，最后乘起来

基环树的部分

基环树上的链肯定是得压到环里的，对着图手玩一会就能发现

这个链长度为 l1l_1 ，到下一个链长度为 l2l_2

如果 l2<l1l_2 < l_1 必然塞不下

如果 l1=l2l_1=l_2 刚刚好一种方案

否则的话第一个点隔一个点链和直接连有两种方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
const int N  = 1e5 + 5;
const ll mod = 1e9 + 7;
int n;
int a[N], in[N], st[N], top;
bool inst[N], vis[N], cyc[N];
int len[N];
void dfs(int x) {
    if (vis[x]) {
        if (inst[x]) {
            for (int i = top; i >= 1; i--) {
                cyc[st[i]] = 1;
                if (st[i] == x) {
                    return;
                }
            }
        }
        return;
    }
    vis[x] = inst[x] = 1;
    st[++top]        = x;
    dfs(a[x]);
    inst[x] = 0;
}
int cnt[N];
ll ans = 1;
void pre(int x) {
    int tot = 0, fr = 0, ed = 0, frid;
    while (cyc[x]) {
        ++tot;
        cyc[x] = 0;
        if (len[x]) {
            if (!fr) {
                fr   = tot;
                ed   = tot;
                frid = x;
            } else {
                int pm = (len[x] < tot - ed) + (len[x] <= tot - ed);
                ans    = 1ll * ans * pm % mod;
                ed     = tot;
            }
        }
        x = a[x];
    }
    if (!fr) {
        ++cnt[tot];
    } else {
        int kl = (len[frid] < tot - ed + fr) + (len[frid] <= tot - ed + fr);
        ans    = 1ll * ans * kl % mod;
    }
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        ++in[a[i]];
    }
    queue<int> q;
    for (int i = 1; i <= n; i++) {
        if (!vis[i])
            dfs(i);
        if (!in[i]) {
            q.push(i);
        }
    }
    for (int i = 1; i <= n; i++) {
        if ((cyc[i] && in[i] > 2) || (!cyc[i] && in[i] > 1)) {
            cout << 0;
            exit(0);
        }
    }
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        len[a[x]] = len[x] + 1;
        if (!cyc[a[x]]) {
            q.push(a[x]);
        }
    }
    for (int i = 1; i <= n; i++) {
        if (cyc[i]) {
            pre(i);
        }
    }
    static ll num[N];
    for (int i = 1; i <= n; i++) {
        if (cnt[i]) {
            num[0] = 1;
            for (int j = 1; j <= cnt[i]; j++) {
                if (i > 1 && i % 2 != 0) {
                    num[j] = (num[j - 1] + num[j - 1]) % mod;
                } else {
                    num[j] = num[j - 1];
                }
                if (j > 1) {
                    num[j] =
                        (1ll * num[j] + 1ll * num[j - 2] * 1ll * (j - 1ll) %
                                            mod * 1ll * i % mod) %
                        mod;
                }
            }
            ans = 1ll * ans * num[cnt[i]] % mod;
        }
    }
    cout << ans << endl;
    return 0;
}
// Asusetic eru quionours