2021.09.18模拟赛

今古恨，几千般，只应离合是悲欢？江头未是风波恶，别有人间行路难。

2021.09.18模拟赛

全 是 J O I

A. 愉快的标志设计

愉快的标志设计

签到题，枚举某一个位置作为起点，前缀和记录下需要改多少个数 $O(n\log n)$ 判断即可

code

B. 电报

电报

贪心蛮好想的，但是不太好证

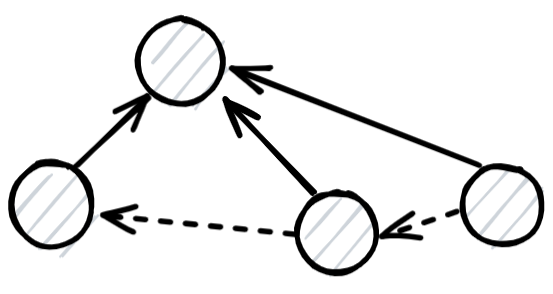
因为每个点只有一个出边，所以最后的强连通分量必然是个环

那么每个点就只能有一个入度

担心的考虑每个点要代价最大的入度，因为这样改的最少

然后考虑会剩下很多环和挂上边的链

要把链并进环里，必然要把链 $a \rightarrow$ 环 的边连上，然后把被连的的点原来的入度拆掉

所以跑一下环，找到这个代价的最小值即可

证明考虑构造出方案来

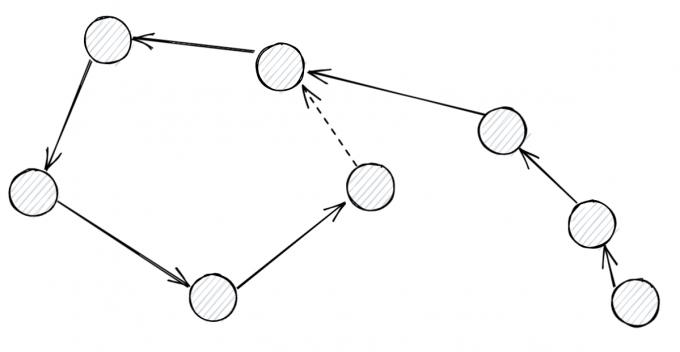
首先这个图会是一个内向基环树森林

我们先把环上的树处理掉，考虑一个节点的两个入度，选择一个最大的入度，然后其他的入度顺次连接就能变成链

然后一个内向基环树，如果最后变成了这样

那他已经变成链了，不用管他

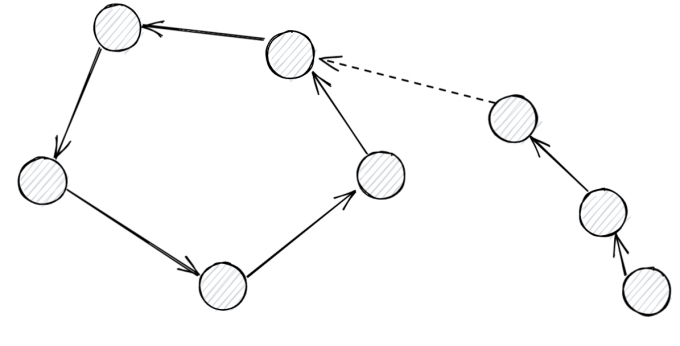
否则就是

那我们贪心找一下断开的环边，也会变成链，最后就是一堆链

随便连就能连出来环

code

C. 三明治

三明治

考虑 $O(n^4)$ 大暴力，枚举每一个点那个位置先被吃，然后爆搜，如果搜出来环就不合法

仔细思考一下能够发现，如果先吃的是左边的，那么它左边的也一定被先吃，所以可以继承状态，对于每一行枚举从左还是从右开始吃

然后每行共用一个 $O(nm)$ 的状态，总复杂度 $O(n^2m)$

code

D. 绳

绳

题面描述比较诡异，其实就是在绳子上找个位置对折一下，要求对应位置颜色对齐

因为染色代价先染后染一样，所以最开始染成两种颜色即可

一个结论是能够折成长度为二的绳子，除了首尾的极大同色连续段都是偶数长度的，充分性显然，必要性可以反证

这能推出来所有同色连续段的首位奇偶性相同，所以枚举奇偶性进行染色，然后剩下的位置选一个颜色最多的染上就行

剩下位置颜色最多的可以开桶维护

code