2021.09.06模拟赛

Per Aspera Ad Astra

2021.09.06模拟赛

A.都市

都市

考虑要升序输出，把升序的答案数组记作 $\{a_i\}$

先把所有的数字排个序，前两个数字必然是 $a_1+a_2$ 和 $a_1+a_3$

但是第三个数字不一定是 $a_2+a_3$ ，但只要知道了 $a_2+a_3$ 是谁就可以直接找出来所以的数字了

所以直接枚举 $a_2+a_3$ 是谁就可以递推了，复杂度 $O(n^3)$

code

B. 争辩

争辩

很妙的题目

仔细考虑题目中的限制条件，先考虑 $a$ 是一个排列的情况，比较明显的能发现逆序对数每次减少 $0$ 或 $2$ 个

所以当且仅当它的逆序对数是奇数它是不优美的

而 $a$ 不是一个排列的话，我们可以用那个重复的元素任意的减少逆序对数（我死在这里）

所以只需要算出来 $det(A)$ 和 $perm(A)$ 然后 $\dfrac{\mathrm{perm}(A)-\det(A)}{2}$ 就是所有不优美的和

$\mathrm{perm}(A) = \sum\limits_{p是排列}\prod A_{i,p_i}$

这个东西叫 积和式 无多项式复杂度做法，但是给出的矩阵很特殊，是一个下三角矩阵加上一条对角线

考虑如果是下三角矩阵显然是所有对角线元素的积

但是加上这一条对角线后就需要考虑其他情况

设大小为 $n$ 的这种矩阵的积和式为 $D_n$

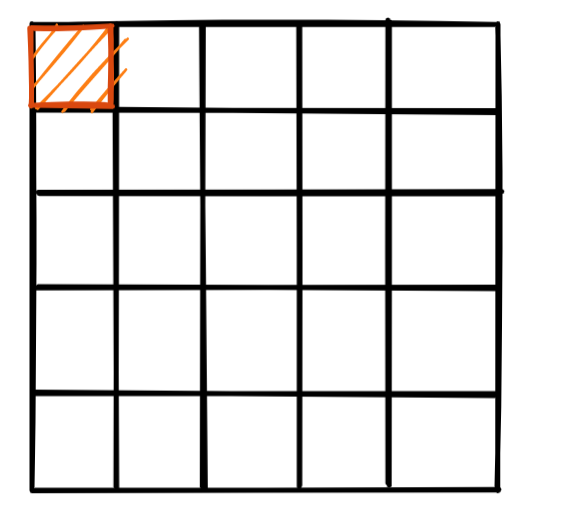
考虑选了第一行的第一个数，有 $D_n = D_{n-1}A_{1,1}$

如果选了第二个

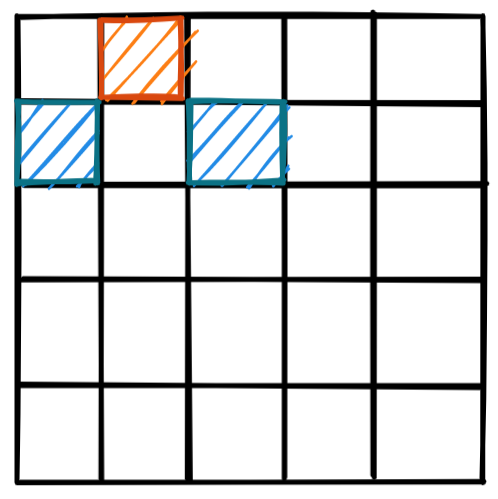
下一行就要选两个蓝色的位置，第一个是 $D_{n-2}A_{2,1}A_{1,2}$ ,第二个需要继续讨论

所以就可以递推下去

加了一条对角线的 $\det(A)$ 也可以这么算

code

C.Prime

Prime

区间筛板子

code

D.Hunter

Hunter

因为期望具有线性性，所以考虑每个人在 $1$ 之前死的概率求和 $+1$ 即可

答案为 $\sum\dfrac{w_i}{w_1+w_i}$

部分分极具误导性

code